Right riemann sum
by jvadair
arrow_back_ios_new
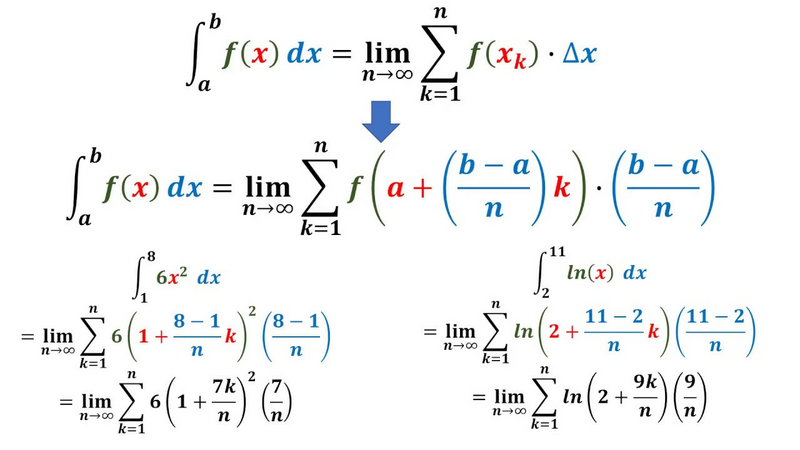
\int_a^bf\left(x\right)dx\ =\ \lim_{n\rightarrow\infty}\sum_{k=1}^nf\left(\frac{b-a}{n}k\right)\cdot\frac{b-a}{n}\
\int_a^bf\left(x\right)dx\ =\ \lim_{n\rightarrow\infty}\sum_{k=1}^nf\left(x_k\right)\cdot\Delta x
arrow_forward_ios
arrow_back_ios_new
arrow_forward_ios
expand_more Scroll for list view... expand_more
2 cards
| 1 | 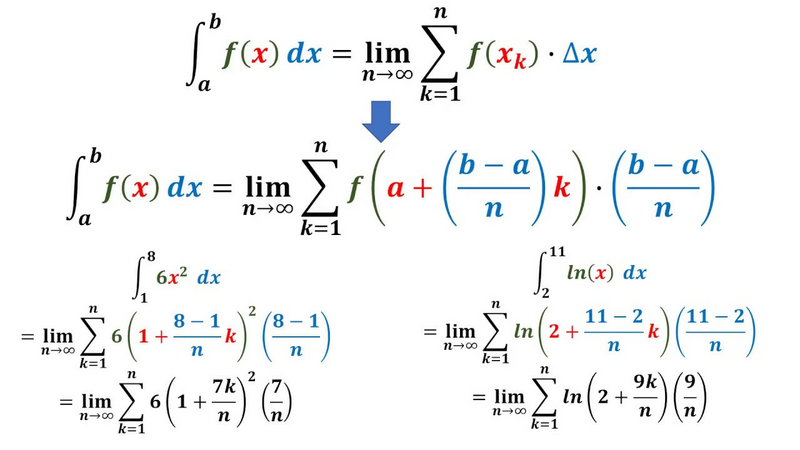 \int_a^bf\left(x\right)dx\ =\ \lim_{n\rightarrow\infty}\sum_{k=1}^nf\left(\frac{b-a}{n}k\right)\cdot\frac{b-a}{n}\ |
\int_a^bf\left(x\right)dx\ =\ \lim_{n\rightarrow\infty}\sum_{k=1}^nf\left(x_k\right)\cdot\Delta x |
| 2 | x^2 |
x^2 |
